The cssr package implements cluster stability selection (Faletto and Bien 2022), a feature selection method designed to allow stability selection to work effectively in the presence of highly correlated features.

Installing the cssr Package

You can install the cssr package using the following command:

remotes::install_github("gregfaletto/cssr-project", subdir = "cssr")

An Introduction to the Package

Given data (X,y), cluster stability selection selects the variables in X that are useful for predicting y.

library(cssr)
# Set seed for reproducibility
set.seed(983219)
# Generate some data containing clusters of highly correlated features
data <- genClusteredData(n = 80, # Sample size
                         p = 40, # Number of features 
                         cluster_size = 10, # Number of features in a cluster correlated with a latent variable
                         k_unclustered = 10, # Number of unclustered features that influence y
                         snr = 3 # Signal-to-noise ratio in the response y generated from the data.
                         )

X <- data$X
y <- data$y

output <- cssSelect(X, y)

output$selected_feats

I’ll first walk through a description of stability selection (Meinshausen and Bühlmann, 2010), the method that cluster stability selection builds on. Then I’ll illustrate a problem with stability selection when data with clusters of highly correlated features are observed. This problem motivates cluster stability selection. Finally, I’ll demonstrate how to use the cssr package to implement cluster stability selection. The cssr package is written with over 3400 tests ensuring that it functions exactly the way we intended when we wrote the paper.

Stability Selection

Cluster stability selection is an extension of stability selection (Meinshausen and Bühlmann, 2010). Stability selection is a procedure deisgned to make any feature selection procedure more stable. Given a data set (X,y) with n observations, stability selection works as follows:

The data are divided into B subsamples of size n/2 (typically, B might be around 50 or 100).
The desired feature selection method is run on each subsample, yielding B selected sets of features.
For each feature, we count how many times it was selected and divide by B to get a selection proportion. We interpret the selection proportion for each feature as a measure of feature importance–the higher the selection proportion is for a feature, the more relevant we think it is for predicting y.
Finally, we use the selection proportions to get a selected set (for example, by taking the top s features for some predetermined s).

The below diagram (from Faletto and Bien 2022) demonstrates the procedure. In the diagram, the lasso is the chosen feature selection procedure, and a selected set is chosen by choosing all features with selection proportions larger than a predetermined τ.

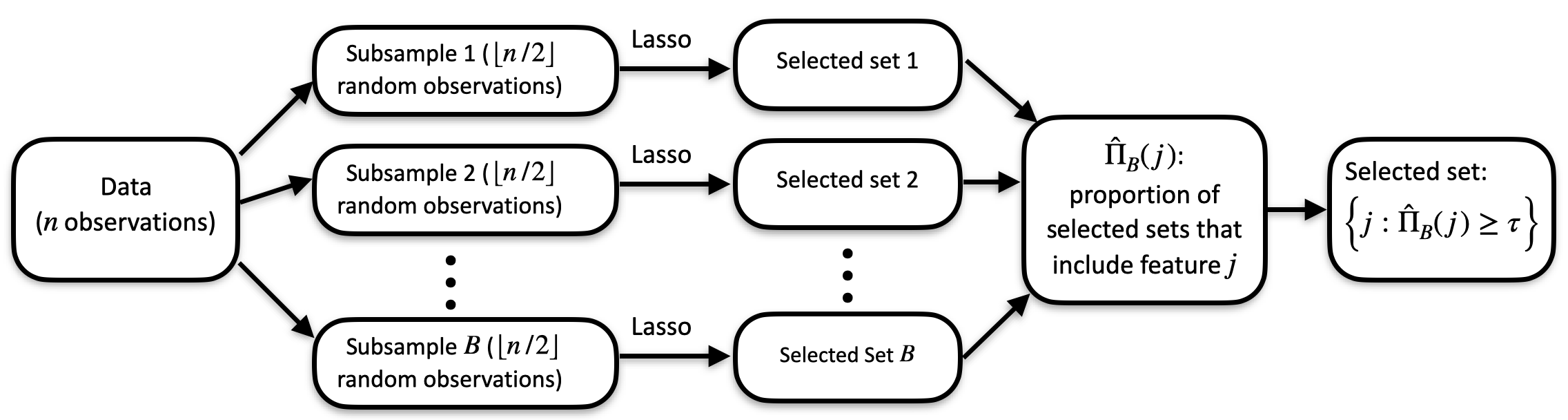
Stability Selection Flowchart Figure

In the classic framework of bias/variance tradeoff, we can think of stability selection as a way to reduce variance at the price of increasing bias. We get a more stable and robust (lower variance) feature selection procedure because we average over many subsamples. The price we pay is that each selected set is estimated using a sample of size n/2 rather than n.

Why Cluster Stability Selection?

Stability selection doesn’t do well when features are highly correlated. The problem is that if there are clusters of highly correlated features, any one member of the cluster might be a reasonably good choice for a predictive model. So the base feature selection might select one cluster member more or less at random. Then at the end, no one cluster member will have a high selection proportion, so no cluster member will be selected as an important feature, even if every selected set contained a cluster member. This problem has been called “vote-splitting.”

In our paper, we walk through an example where there is a latent (unobserved) feature Z that is important for predicting y. Z is not observed, but 10 proxies for Z are observed–features that are highly correlated with Z (and therefore with each other, too). There are also 10 “weak signal” features that influence y, but less so than Z. We show in a simulation study that stability selection tends to end up with low selection proportions for the proxies for Z, even though any one of the Z proxies would be more useful for predicting y than all of the “weak signal” features.

The below figure shows the selection proportions yielded by stability selection for proxies for Z, “weak signal” features, and “noise” features that are unrelated to y.

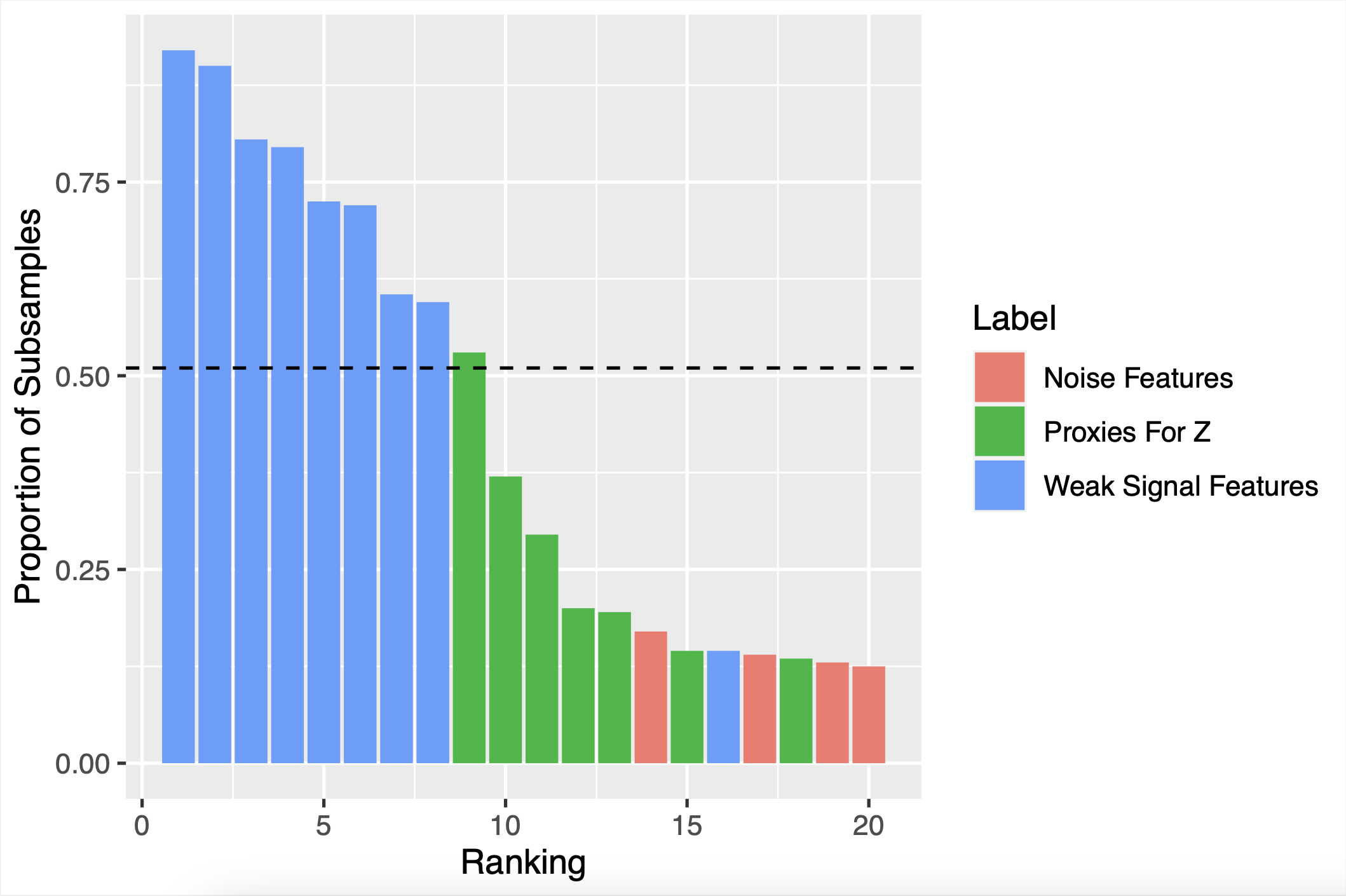
Selection Proportions

How does cluster stability selection fix this?

Cluster stability selection modifies stability selection with a simple fix: instead of only keeping track of the individual feature selection proportions, we also keep track of the cluster selection proportions–the proportion of subsamples in which at least one cluster member was selected. Then we can rank clusters by their importance according to cluster selection proportion, and select entire clusters. This avoids the vote-splitting problem!

Getting started with selecting features by cluster stability selection using the cssSelect function

The data we generated at the beginning of third document contain a cluster of 10 features (specifically, the first 10 columns of X) that are highly correlated both with each other and also with an unobserved variable Z that is associated with y. The cssSelect function in the cssr package yields a set of features selected by cluster stability selection. We can tell cssSelect about the cluster using the “clusters” argument.

clus_output <- cssSelect(X, y, clusters=list("Z_cluster"=1:10))

This input tells cssSelect that features 1 through 10 are in a cluster, and it names the cluster “Z_cluster” (providing a name is optional and is only for your convenience). cssSelect returns both a set of selected clusters (below) and all of the features contained within those clusters (as in the above).

clus_output$selected_clusts

clus_output$selected_feats

By default, cssSelect decides how many clusters to select on its own. However, you can set this yourself using the max_num_clusts argument.

clus_output_three <- cssSelect(X, y, clusters=list("Z_cluster"=1:10),
  max_num_clusts=3)
  
clus_output_three$selected_clusts

You can also select all of the clusters with selection proportion above a certain threshold, rather than selecting a pre-specified number of clusters.

clus_output_3 <- cssSelect(X, y, clusters=list("Z_cluster"=1:10),
  cutoff=0.3)
  
clus_output_3$selected_clusts

cssSelect uses the lasso (as implemented by the R glmnet package) as the base feature selection procedure. The lasso requires a tuning parameter λ. cssSelect will choose λ automatically by default, but you can also provide your own λ value if you’d like. (Remember that λ should be chosen for subsamples of size n/2.)

clus_output_lam <- cssSelect(X, y, clusters=list("Z_cluster"=1:10),
  lambda=0.01, cutoff=0.3)

Getting more advanced: the css function

Cluster stability selection is computationally intensive because it involves running a feature selection algorithm B times. Because of that, if you are going to use one data set and play around with the results (for example, by trying different model sizes or cutoffs), it is more efficient to only do the feature selection step once and then use the results however you want. The function css isolates this computationally intensive set and provides a convenient output that can be easily used by other functions in the package.

The css function is both more flexible and more demanding than cssSelect. In particular, css requires you to specify a lambda. If you’re not sure how you want to choose a lambda, we provide a function getLassoLambda that will do it for you.

lambda <- getLassoLambda(X, y)
# Notice that the below function call takes kind of a long time. (cssSelect has to call css internally every time it is used.)
css_output <- css(X, y, lambda, clusters=list("Z_cluster"=1:10))

str(css_output)

The css function outputs an object of class cssr, a list containing the following elements:

feat_sel_mat: A 2 ⋅ B × p matrix of feature selection indicators. (feat_sel_mat[i, j] equals 1 if feature j was selected on set i and 0 otherwise.) feat_sel_mat is used to calculate the feature selection proportions.
clus_sel_mat: Like feat_sel_mat, except its number of columns is equal to the number of clusters, and it contains indicators of whether each cluster was selected on each subsample. clus_sel_mat is used to calculate the cluster selection proportions.
X (the originally provided X is returned)
y (the originally provided y is returned)
clusters (a list of clusters is returned; any features that were not specified to be in a cluster in the function input will be put in their own “cluster” of size 1, and any unnamed clusters will automatically get their own names).
train_inds (don’t worry about this for now)

css has more options than cssSelect. Here are some of the options:

You can select your own number of subsamples to use B. Larger values of B may be a bit more robust, but will require more computation time. (Also, there will be diminishing returns past a certain point, since there are only n data points to work with no matter how large B gets.) The default B is 50, leading to 100 subsamples.
You can specify your own feature selection function, fitfun. This must be a function that accepts as arguments X, y, and lambda (the lambda argument can be ignored if you like) and it must return an integer vector (containing the indices of the features selected using the data). Other than those requirements, the function can be whatever you want! Here’s one example of a valid (but silly) fitfun that ignores lambda and chooses p/2 features at random:

testFitfun <- function(X, y, lambda){
    p <- ncol(X)
    # Choose p/2 features randomly
    selected <- sample.int(p, size=floor(p/2))
    return(selected)
  }
  
css_output_test <- css(X, y, lambda, clusters=list("Z_cluster"=1:10),
  fitfun=testFitfun, B=10)

str(css_output_test)

Here’s another that requires lambda to be an integer and takes the top lambda features with the highest absolute correlations with y. (Lambda can be anything you want and mean whatever you want, it’s up to you!)

corFitfun <- function(X, y, lambda){
    cors <- as.vector(abs(cor(X, y)))
    names(cors) <- 1:ncol(X)
    cors <- sort(cors, decreasing=TRUE)
    selected <- as.integer(names(cors[1:lambda]))
    return(selected)
  }
  
css_output_cor <- css(X, y, lambda=8, clusters=list("Z_cluster"=1:10),
  fitfun=testFitfun, B=10)

str(css_output_cor)

Getting selected feature sets using getCssSelections

The function getCssSelections gets sets of selected features from the output of css. (This function is much faster to call than cssSelect since it relies on the already-generated output from css.)

sels <- getCssSelections(css_output, max_num_clusts=5)

sels

You can choose a selected set according to a few criteria that you can provide as function inputs:

Set a cutoff to select only features whose selection proportions are at least as large as the cutoff.
Set min_num_clusts to ensure that at least min_num_clusts features are returned (regardless of cutoff)
Set max_num_clusts to ensure that at most max_num_clusts are returned (regardless of cutoff, and if fulfilling min_num_clusts and max_num_clusts at the same time is impossible, max_num_clusts gets priority).

getCssSelections(css_output, cutoff=0.7)

getCssSelections(css_output, cutoff=0.99, min_num_clusts=12)

getCssSelections(css_output, cutoff=0.5, min_num_clusts=3, max_num_clusts=7)

For more information…

Thank you for reading this far! I intend to add more to the vigenette later. For now, you can learn more about the package by reading the bookdown that defines the package here.